You may not remember much from your high school algebra class, but the Pythagorean Theorem may still ring a bell. This was the easiest algebraic formula to remember and the one that dealt with right angles.
Your high school algebra teacher probably explained that this formula was named after the Greek mathematician who developed it. But a recent discovery on an ancient Babylonian clay tablet shows that this knowledge was ancient even before Pythagoras’s time.
The Pythagorean Theorem, A Building Block of Mathematics
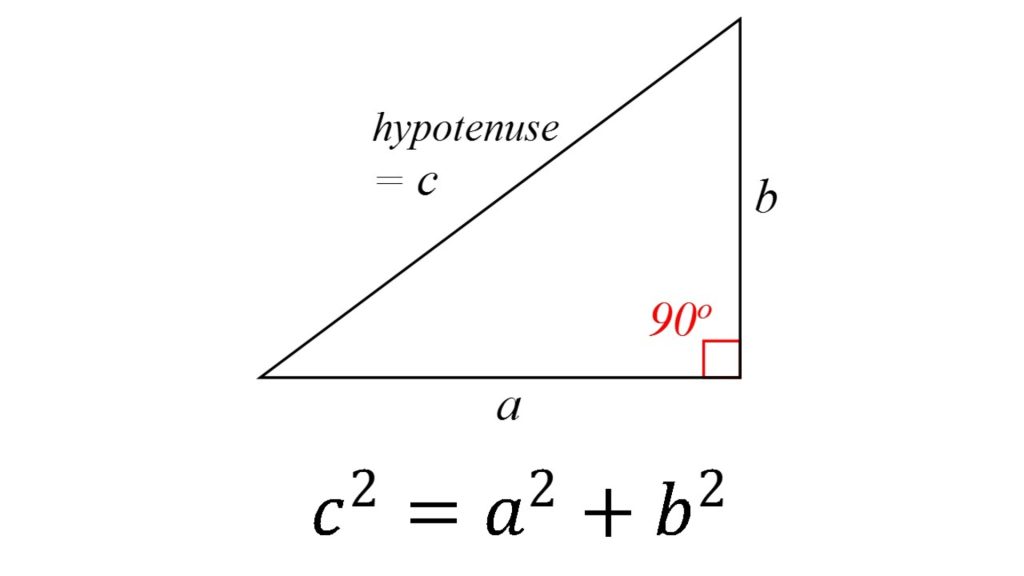
The Pythagorean Theorem tells us that when we have a right-angled triangle, the square of the side that is opposite of the right angle, the hypotenuse, is equal to the square of the other two sides. To put it into math language, a2+b2=c2.
In algebra class, this formula meant nothing but homework. In the real world, however, the Pythagorean Theorem has plenty of practical applications beyond geometry and trigonometry. Engineers, architects, graphic designers, land surveyors, and more put the Pythagorean Theorem to good use every day.
Just Who Was Pythagoras?
Pythagoras was born on the island of Samos sometime around the year 570 BC. Like most ancient Greeks, he was a man of many interests. He was a scholar, theologian, philosopher, astronomer, musician, teacher, and mathematician. An influential and charismatic man, he attracted devout followers.

Pythagoras developed his philosophical teachings into Pythagoreanism, a belief system that was one part cult and one part math lesson. He preached that mathematics paved the way to living in harmony with the cosmos. Practitioners of Pythagoreanism believed the soul was immortal and the dead would be reincarnated.
Pythagoras and His Famous Theorem
Unfortunately, all of Pythagoras’s original writing has been lost to time. A group of devoted followers carried on his teachings at a school he founded in southern Italy called the Semicircle of Pythagoras. This was a secret group – again, a bit cult-like – in which knowledge was verbally passed from one generation to the next.

According to mathematician Bruce Ratner, “Out of respect for their leader, many of the discoveries made by the Pythagoreans were attributed to Pythagoras himself; this would account for the term ‘Pythagoras’ Theorem’.”
The Theorem Was Not His Original Work
So, despite centuries of teachings that say otherwise, it is very likely that the Pythagorean Theorem was not Pythagoras’s original work. Math scholars have long suspected this, but they thought it was impossible to prove.

But a translation of a much older clay tablet is giving us the evidence we need to prove that Pythagoras is getting undue credit for the fundamental mathematical formula that bears his name.
The Ancient Babylonians Knew About the Pythagorean Theorem Before Pythagoras Was Born
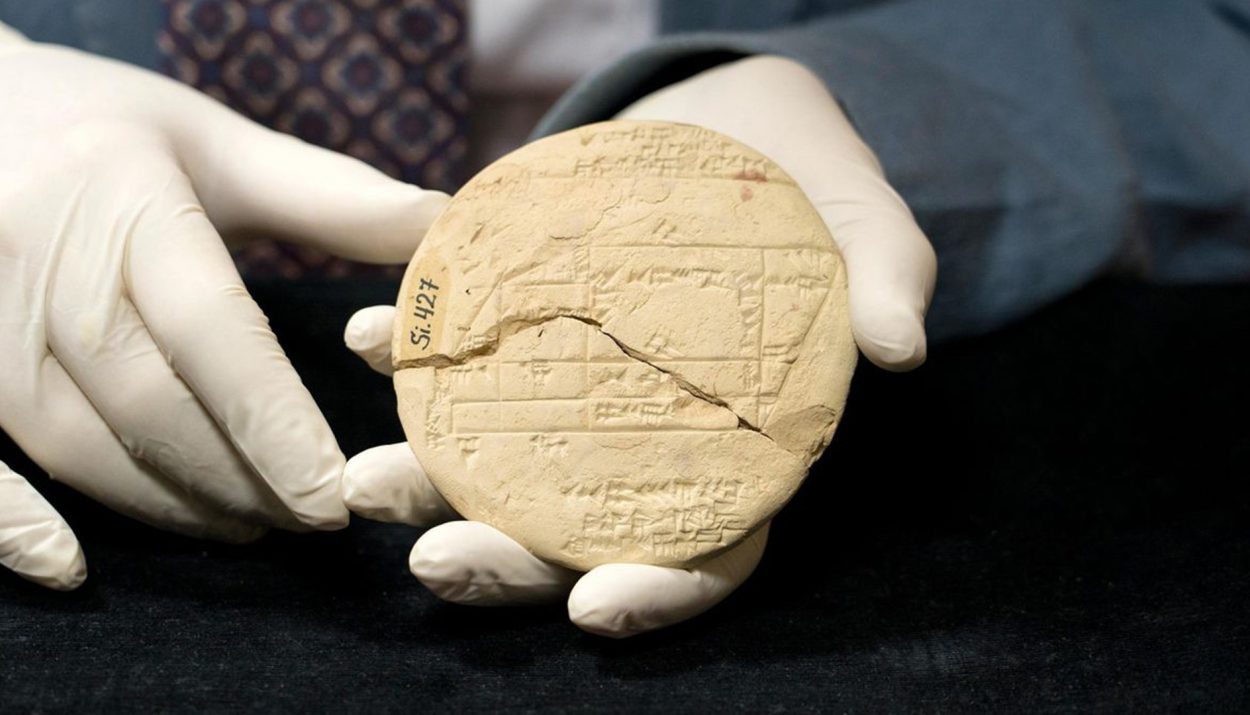
In 1894, a team of archaeologists from France conducted a dig in present-day Iraq and unearthed a clay tablet with cuneiform writing on it. The tablet, named Si.427, is now part of the permanent collection at the Istanbul Archeological Museum in Turkey.

The Si.427 tablet is about 3,700 years old and was created by the ancient Babylonians who lived in the region. The age of this tablet predates Pythagoras’s birth by more than 1,000 years.
The Message on the Tablet
Mathematician Daniel Mansfield of Australia’s University of New South Wales studied the cuneiform message on the Si.427 tablet and came to a stunning realization. The tablet contained the formula that we now know as the Pythagorean Theorem.

Mansfield said, “It is generally accepted that trigonometry -the branch of math that is concerned with the study of triangles – was developed by the ancient Greeks studying the night sky,” Yet this much older text offered instructions on how to make accurate right triangles.
One Ancient Find Led to the Translation of Another
The Si.427 tablet sat unnoticed for more than a century. Then, in 2017, Mansfield discovered that another cuneiform tablet from the same time period, called the Plimpton 322 tablet, contained a trigonometric table.

That inspired Mansfield to take a closer look at other tablets. That is when he noticed the Pythagorean triplets on the Si.427 tablet. From the inscriptions on both tablets, Mansfield was able to see how the ancient Babylonians were using algebraic formulas to divide parcels of land.
The Babylonians Figured It Out First
After studying Mansfield’s findings and authoring his own paper on the topic, Ratner noted, “The conclusion is inescapable. The Babylonians knew the relation between the length of the diagonal of a square and its side: d=square root of 2.”

As we will soon see, the Si.427 tablet was not an ancient Babylonian high school student’s homework. Nor was it a theoretical math lesson. It had a practical application.
“Applied Geometry“
As Mansfield explained, the Si.427 tablet is the earliest known example of applied geometry. He said, “The Babylonians developed their own alternative ‘proto-trigonometry’ to solve problems related to measuring the ground, not the sky.”

The tablet was, as Mansfield pointed out, the only known example of a cadastral document from the Old Babylonian era. What is a cadastral document? It is a system by which land surveyors plot boundaries. “In this case, it tells us legal and geometric details about a field that’s split after some of it was sold off,” Mansfield explained.
The Details of the Inscription
The Si.427 tablet provides details on a marshland with several structures built on it, such as a tower. There are three sets of numbers on the tablet – 3, 4, 5; 8, 15, 17; and 5, 12, 13 – or what mathematicians call a ‘Pythagorean triple.”

Each of these sets of the numbers, if plugged into the Pythagorean Theorem formula, are correct. The sum of the squares of the first two numbers equals the square of the third number. For example, 32+42=52 or 9+16=25.
Don’t Look for that Familiar Formula
The Si.427 tablet, which was likely used to set land borders, does not contain the familiar a2+b2=c2 formula that we associate with the Pythagorean Theorem. Perhaps this is why the tablet’s importance went unnoticed for so long.

The Si.427 tablet, with its Pythagorean triplets, does tell us that the ancient Babylonians had an understanding of the general principles of geometry and how it could be put to practical use. As Ratner observed, “This means that they were familiar with the Pythagorean Theorem more than a thousand years before the great sage for whom it was named.”
Using Math to Settle Land Disputes
The Si.427 tablet gives us a clue to tell us why it was important for the ancient Babylonians to accurately plot land boundaries. The tablet makes mention of a land dispute between a wealthy and unnamed female landowner and a prominent gentleman named Sin-bel-apli.

The dispute between the two involved the ownership of some date palm trees on the border between their two properties. As Mansfield explained, “It is easy to see how accuracy was important in resolving disputes between such powerful individuals.”
Good Boundaries Make Good Neighbors
According to Mansfield, the time period in which the Si.427 tablet was created coincides with the rise of land ownership in ancient Babylon. It was becoming important to be able to differentiate between plots of land.
He said, “This is from a period where land is starting to become private – people started thinking about land in terms of ‘my land and your land’, wanting to establish a proper boundary to have positive unneighborly relationships.”